knowledge-base

The Big O Notation

The big O notation is used to express time complexity, the time it takes to execute, time being expressed as the amount of steps required relative to the size of the data set it works on. This is usefull to objectivly quantify how good an algorithm is in regarding to the max CPU capacity.

We can use the Big O notation also for the space complexity, the amount of memory is required to execute the algorithm relative to the size of your data set. This is particularly usefull when you are constraint to the amount of memory on your machine.

We use this notation to efficiently communicate the efficiency of a given algorithmn.

Time Complexity

We express the steps taken in relation to the size of the data set, so the amount of elements in your data set to execute given algorithm.

Keep in mind, we express the amount of steps taken to calculate the algorithm, but the execution time is relative still as it strongly depends on the speed of the machine that will execute all the steps.

So an algorithm might take longer on one machine than the other if their CPU speed differs.

Space Complexity

For N elements of data, an algorithm consumes a relative number of additional data elements in memory.

Constants

Note that in a Big ) notation we ignore constants. Meaning, if an algorithm takes consistently 3 steps, regardless of the amount if elements. We will say O(1). This is because the constants might be non trivial on a very small data set, we are mostly curious on how an algorithms performs on a large set of data. At this point constants become trivial in comparison to the size of the data set.

Therefore we’ll never see O(3), we will always express this as O(1).

Different scenarios

Often algorithms will perform different depending on the number of elements. That’s why often will quantify an algorithm with the Big O notation for different scenarios.

• The Best Case Scenario
• The Average Case Scenario
• The Worst Case Scenario

By default a Big O notation refers to the worst case scenario unless specified otherwise.

Logarithms

Logarithms are the inverse of exponents

O(log N) means that the algorithm takes as many steps as it takes to keep halving the data elements we we remain with one.

e.g. Log2 8 = 3 as ` 8 / 2 / 2 = 1`

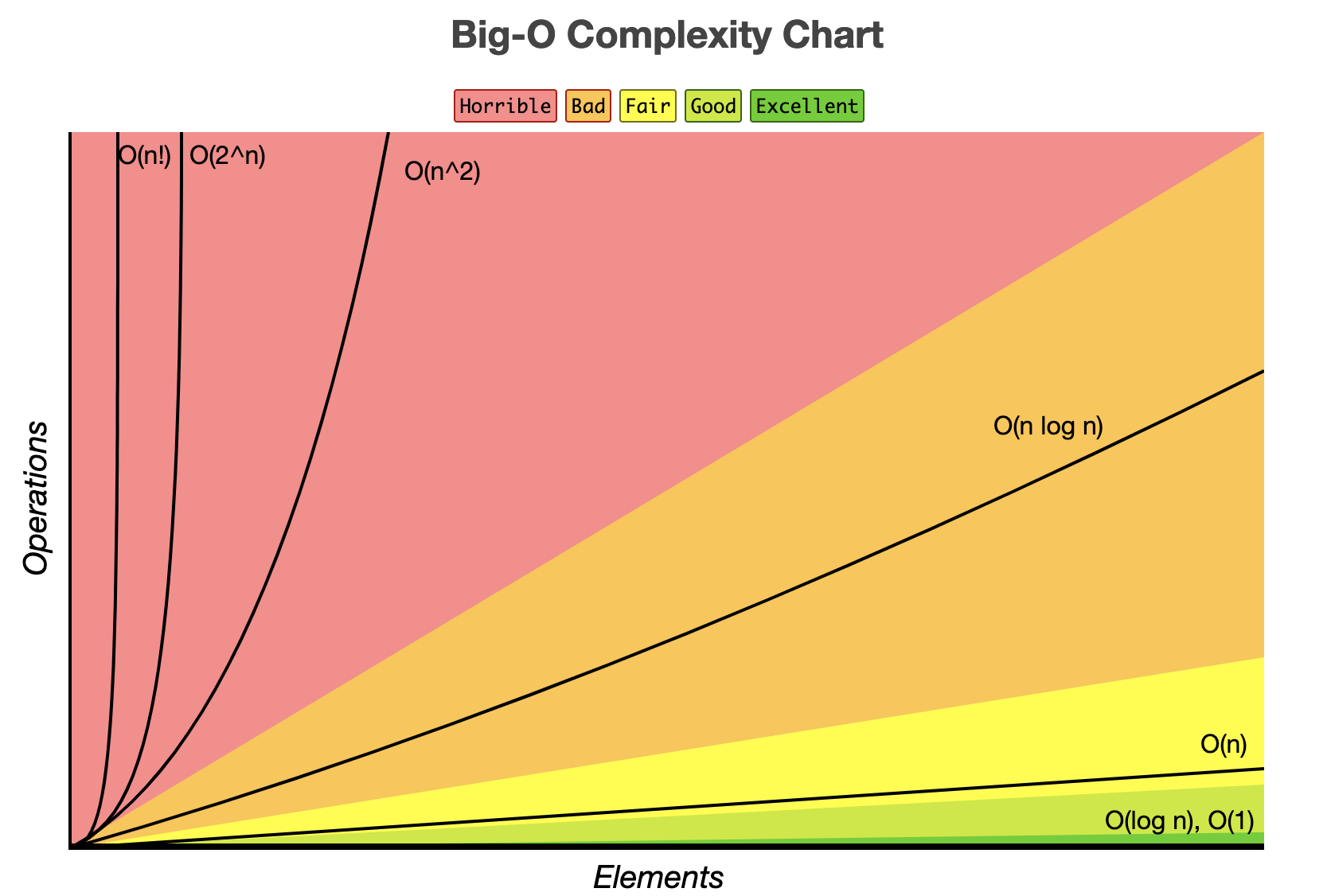
Comparison

This chart shows the comparison of different Big 0 notations.

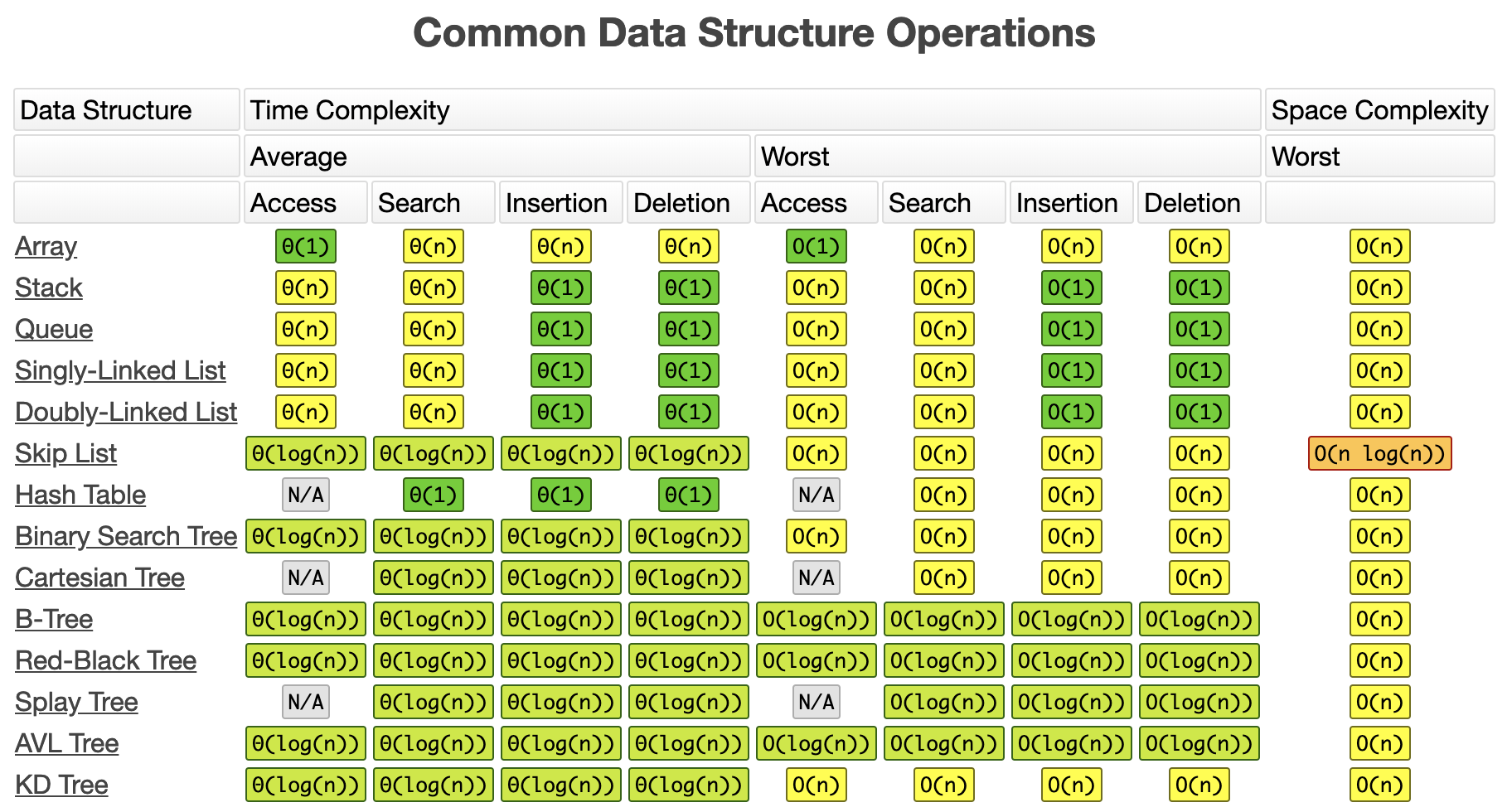
This chart show the efficiency of Data Structure operations

Do note that some values are not correct for linked lists.

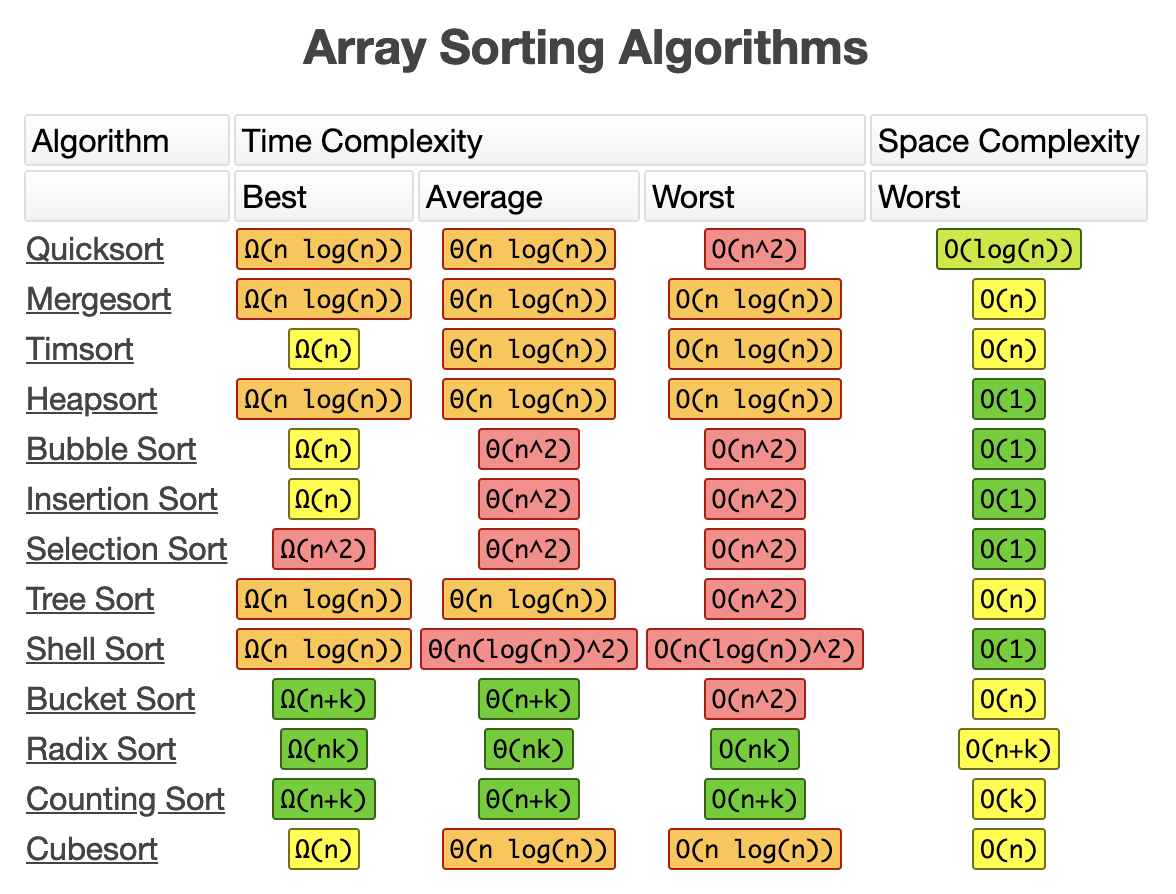
This chart show the efficiency of sorting algorithms

In Depth

• When we work with data sets large enough so that only the order of growth of the time that it takes to run an algorithm becomes relevant we are studying the asymptotic efficiency of algorithms, we use asymptotic notations for that. These notations are applied on functions (e.g an² + bn + c) and abstract away details of the function.

• Asymptotic notation can be used for different charachteristics of an algorithm, usually the running time (time complexity) but also on for example the memory usage (space complexity) and others.

• We have different asymptotic notations

  • Θ (theta) notation
  • O (big oh) notation
  • Ω (big omega) notation
  • o (little oh) notation
  • ω (little omega) notation

The different asymptotic notations explained

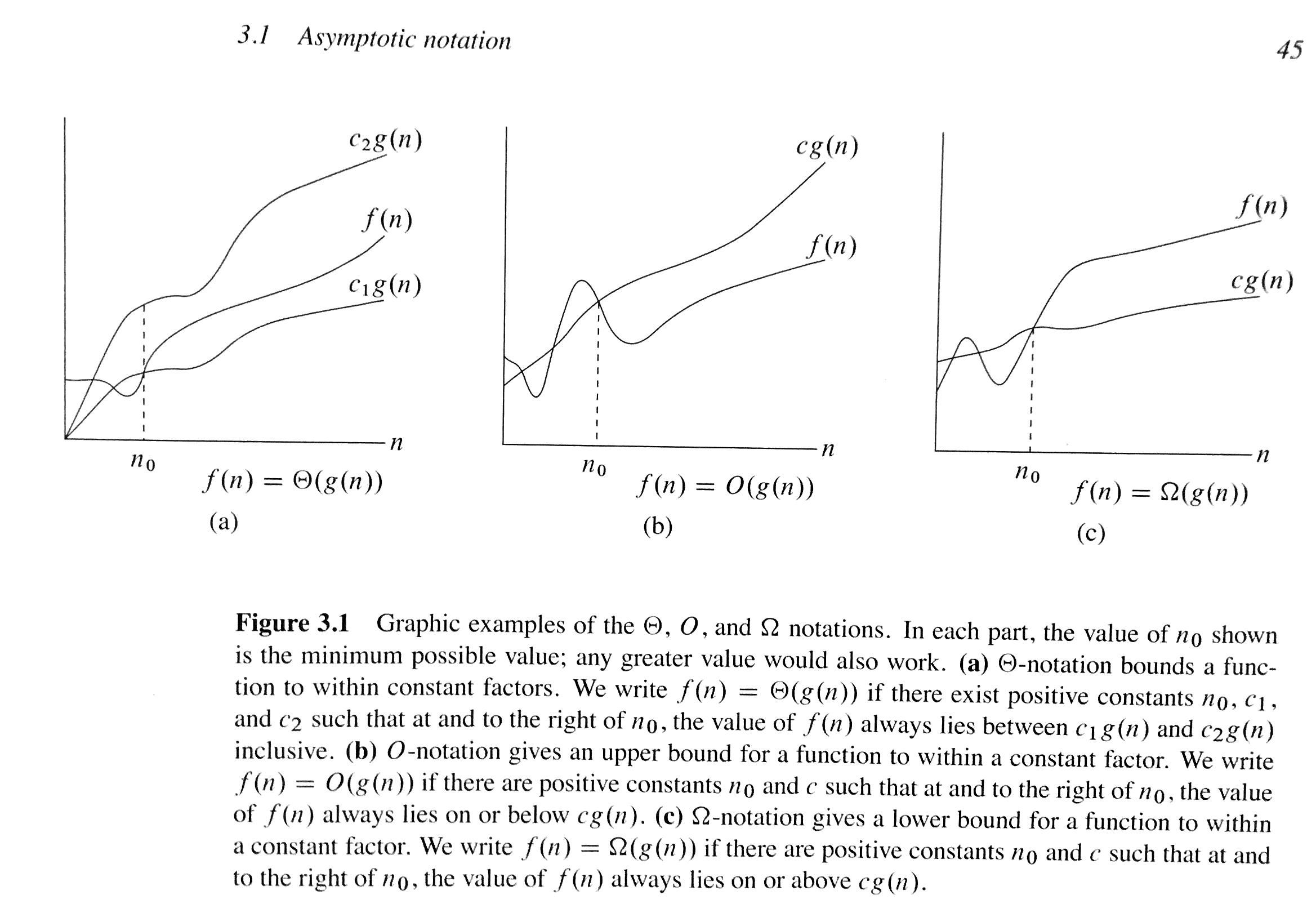Source: Introduction to algorithms

Let’s say we have a function g that operates on n amount of items. We can then express if a function f(n)

Θ (theta) notation

Bounds a function from above and below

• For a given function g(n) we indicate with Θ(g(n)) the set of functions. A function f(n) belongs to the set Θ(g(n)) (aka f(n) ∈ Θ(g(n))) if there exist positive constants c₁ and c₂ such it can be “sandwiched” between c₁ g(n) and c₂ g(n).
• g(n) is an asymptoticly tight bound for f(n)
• Every member of the set Θ(g(n)) must be asymptoticly nonnegative, meaning f(n) is nonnegative whenever n is sufficiently large. We don’t say asymptoticly positive as an asymptoticly positive function is one that is positive for all sufficiently large n.
• Point being, f(n) ∈ Θ(g(n)) means that our function falls between a certain upper and lower bound (Carefully stated by myself).
• This notation tends to be used for the average-case running time of an algorithm (see the chart at the top).

O (big oh) notation

When we have only an asymptotic upper bound

• Basically f(n) ∈ O(g(n)), meaning for all values n at and the right of n₀, the value of the function f(n) is on or below c g(n).
• Note f(n) ∈ Θ(g(n)) implies f(n) ∈ O(g(n)). As the value for f(n) must be on or below the value of O(g(n)) and fall within the margins of O(g(n)).
• Distinguishing asymptotic upper bounds from asymptotically tight bounds is standard in algorithms literature.
• We are giving a upper bound on the worst-case running time of an algorithm.

Ω (big omega) notation

When we have only an asymptotic lower bound

• For all values n at or to the right of n₀, the value of f(n) is on or above the c g(n).
• We are giving a lower bound on the best-case running time of an algorithm.

o (little oh) notation

• The asymptotic upper bound may or may not be asymptotically tight.
• The little o notation indicates an upper bound that is not asymptotically tight.

ω (little omega) notation

• The asymptotic lower bound may or may not be asymptotically tight.
• The little omega notation indicates an lower bound that is not asymptotically tight.

Putting it together with an analogy

• f(n) = O(g(n)) is like a <= b
• f(n) = o(g(n)) is like a < b
• f(n) = Θ(g(n)) is like a = b
• f(n) = Ω(g(n)) is like a >= b
• f(n) = ω(g(n)) is like a > b